Résolution d'équations différentielles¶

Utilisation du module scipy pour résoudre les équations différentielles linéaires.

Pour cela on utilise la fonction solve_ivp du module scipy.

solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None)

Les paramètres sont :

Paramètre	Description
fun	Fonction qui définit notre système. L'appel est de la forme `fun(t, y)`.
t_span	Intervalle d'intégration sous la forme `[t0,tf]`.
y0	État initial du système.
method	Méthode d'intégration. Par défaut, utilise `RK45`. On peut aussi utiliser : `RK23`, `DOP853`, `Radau`, `BDF`, `LSODA`. On utilise les méthodes `RK45, RK32 et DOP853` pour les problèmes d'équations différentielles non raides et les méthodes `Radau, BDF et LSODA` pour les problèmes d'équations différentielles raides (c'est à dire sensible aux paramètres).
t_eval	Les instants à évaluer. Par défaut, ils sont calculés automatiquement.
dense_output	S'il faut calculer une solution
events	Événements à suivre.
vectorized	Si le problème (`fun`) est mis en oeuvre de manière vectorisée.
arg	Les arguments à passer au problème (`fun`).

La fonction retourne un dictionnaire contenant les champs suivants :

Élément	Description
t	Table contenant les instants temporels.
y	Table de tableau contenant les valeurs de la solution.
sol	La solution trouvée par une instance "OdeSolution".
t_events	Liste de tables qui contient les événements détectés.
y_events	Pour chaque événement de "t_events" correspond la valeur de la solution.

Plus d'info sur la fonction sur le lien suivant solve_ip.

Équation différentielle d'ordre 1¶

Démarche¶

Soit l'équation différentielle suivante : $y'(t)+a\,y(t)+b=0$

On met l'équation sous la forme : $y'(t) = f(t,y(t))$ en précisent sa condition initiale

$\left\{\begin{array}{l} y'(t)=-a\,y(t)-b\\ y(t_0)=y_0 \end{array}\right.$

Cette mise en forme de l'équation différentielle est appelée problème de Cauchy. - On résout ensuite l'équation avec la fonction solve_ivp

from scipy.integrate import solve_ivp
import numpy as np

# Définition de l'équation différentielle
def equation(t, y):
    a = 1
    b = 2
    return -a*y-b


t0 = 0  # seconde
tf = 1  # seconde
y0 = 0  # Condition initiale

# Résolution
solution = solve_ivp(equation, [t0, tf], [y0], max_step=0.1)

print(solution.t)  # Affichage de la table des instants
print(solution.y[0])  # Affichage des résultats

[0.000e+00 1.000e-04 1.100e-03 1.110e-02 1.111e-01 2.111e-01 3.111e-01
 4.111e-01 5.111e-01 6.111e-01 7.111e-01 8.111e-01 9.111e-01 1.000e+00]
[ 0.00000000e+00 -1.99990000e-04 -2.19879044e-03 -2.20772446e-02
 -2.10301480e-01 -3.80613812e-01 -5.34718782e-01 -6.74158726e-01
 -8.00329204e-01 -9.14492974e-01 -1.01779263e+00 -1.11126201e+00
 -1.19583662e+00 -1.26424112e+00]

Ancienne fonction¶

Si la fonction solve_ivp n'est pas disponible, ce qui est possible sur les anciennes versions du module scipy, vous pouvez utiliser la fonction odeint.

from scipy.integrate import odeint
import numpy as np

# Définition de l'équation différentielle
def equation(y, t):  # Attention inversion de t et y
    a = 1
    b = 2
    return -a*y-b

t0 = 0
tf = 1  # seconde
y0 = 0  # Condition initiale
t = np.linspace(t0, tf, 11)  # Création des instants de cacluls

# Résolution
y = odeint(equation, y0, t)

print(t)  # Affichage des instants t
print(y[:, 0])  # Affichage des résultats

[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
[ 0.         -0.19032515 -0.36253849 -0.51836355 -0.65935989 -0.78693866
 -0.9023767  -1.00682937 -1.10134207 -1.18686068 -1.26424112]

import matplotlib.pyplot as plt

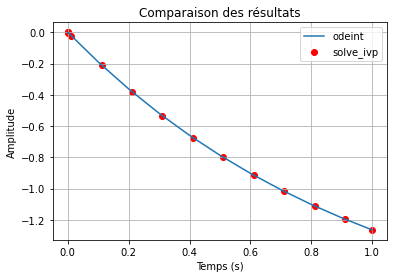
# Tracé des deux résultats
plt.scatter(solution.t, solution.y[0], label="solve_ivp", color="red")
plt.plot(t, y[:, 0], label="odeint")
plt.ylabel('Amplitude')
plt.xlabel("Temps (s)")
plt.title("Comparaison des résultats")
plt.grid(which="both")
plt.legend()
plt.show()

png

Exemple¶

Soit le circuit électrique suivant :

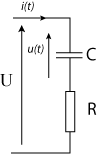
Circuit RC

Aux bornes du générateur, on a l'équation électrique suivante : $u(t)+R\,i(t)=U$
L'intensité est liée à la charge du condensateur par l'équation : $i(t)=\frac{dq}{dt}=C\frac{du(t)}{dt}$
On obtient alors l'équation différentielle suivante :

$u(t)+R\,C\frac{du(t)}{dt}=U$

On la met sous la forme : $\frac{dy}{dt}=f(y)$

$\frac{du(t)}{dt} = \frac{U - u(t)}{R\,C}$

Si le condensateur est initialement déchargé, on à la condition initiale : $u(t=0)=0$

Résolution de l'équation différentielle :

from scipy.integrate import solve_ivp
import numpy as np

# Constantes du système
R = 10  # Ohms
C = 0.01  # F
U = 5  # V

# Définition de l'équation différentielle
def equation(t, u):
    return (U-u)/(R*C)


t0 = 0
tf = 0.8  # seconde
u0 = 0  # Condition initiale

# Résolution
tension = solve_ivp(equation, [t0, tf], [u0])

# Calcul du courant traversant le condensateur
courant = (U-tension.y[0])/R

import matplotlib.pyplot as plt

# Tracé de la tension aux bornes du condensateur
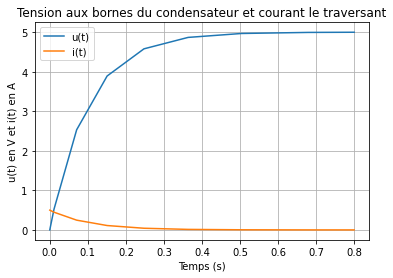
plt.plot(tension.t, tension.y[0], label="u(t)")
plt.plot(tension.t, courant, label="i(t)")
plt.ylabel('u(t) en V et i(t) en A')
plt.xlabel("Temps (s)")
plt.title("Tension aux bornes du condensateur et courant le traversant")
plt.grid(which="both")
plt.legend()
plt.show()

png

Système d'équations différentielles couplées d'ordre 1¶

Démarche¶

Soit le système d'équations différentielles couplées suivant :

$\left\{\begin{array}{l} \frac{dx}{dt}=\sigma\,[y(t)-x(t)]\\ \frac{dy}{dt}=\rho \,x(t)-y(t)-x(t)z(t)\\ \frac{dz}{dt}=x(t)\,y(t)-\beta \,z(t) \end{array}\right.$

Résolution du système :

from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
sigma = 10
rho = 28
beta = 8/3

# Définition des conditions initiales
x0 = 1
y0 = 1
z0 = 1

# Définition du système d'équation différentielle
def systeme(t, Y, σ, ρ, β):
    x = Y[0]
    y = Y[1]
    z = Y[2]

    dx_dt = σ*(y-x)
    dy_dt = ρ*x-y-x*z
    dz_dt = x*y-β*z

    return [dx_dt, dy_dt, dz_dt]


# Résolution
solution = solve_ivp(systeme, [0, 40], [x0, y0, z0], method='RK45', args=(
    sigma, rho, beta), max_step=0.01)

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Récupération des résultats
x = solution.y[0]
y = solution.y[1]
z = solution.y[2]

# Tracé du résultat en 3D
fig = plt.figure()
ax = fig.gca(projection='3d')
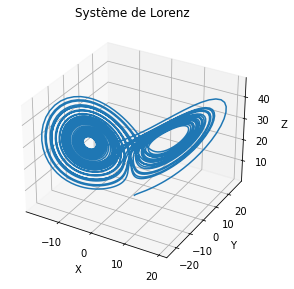
ax.plot(x, y, z, label='Attracteur étrange')
plt.title("Système de Lorenz")
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.tight_layout()
plt.show()

png

Exemple pour une machine à courant continu¶

Soit le modèle suivant de la machine à courant continu :

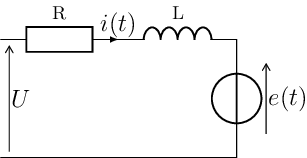
Modèle MCC

L'équation électrique s'écrit :

$U=R\,i(t)+L\,\frac{di(t)}{dt}+e(t)$

Avec $e(t)=K_e\,\omega_m(t)$
On la met sous la forme : $\frac{dy}{dt}=f(y)$

$\frac{di(t)}{dt}=-\frac{R\,i(t)}{L}+\frac{U-K_e\,\omega_m(t)}{L}$

L'équation mécanique de la MCC s'écrit : $J\,\frac{d\omega_m(t)}{dt} = Cm(t)-Cr$ avec $C_m(t)=K_t\,i(t)$
On obtient alors le système d'équations différentielles suivant :

$\left\{\begin{array}{l} \frac{di(t)}{dt}=-\frac{R\,i(t)}{L}+\frac{U-K_e\,\omega_m(t)}{L}\\ \frac{d\omega_m(t)}{dt} = \frac{K_t\,i(t)-Cr}{J} \end{array}\right.$

Résolution du système :

from scipy.integrate import solve_ivp
import numpy as np

# Définition du système
def systeme(t, y):
    # Définitions des constantes du système
    R = 0.345  # Ohms
    L = 0.04e-3  # H
    U = 6  # V
    J = 14.5e-6  # kgm²
    Ke = 1/(1640*np.pi/30)  # Vs/rad
    Kt = 5.84e-3  # Nm/A
    Cr = 0.143*Kt  # Nm

    omega = y[0]
    i = y[1]

    dwdt = (Kt*i-Cr)/J
    didt = -R*i/L+(U-Ke*omega)/L

    return [dwdt, didt]


# Résolution
sol = solve_ivp(systeme, [0, 1.5], [0, 0])

import matplotlib.pyplot as plt

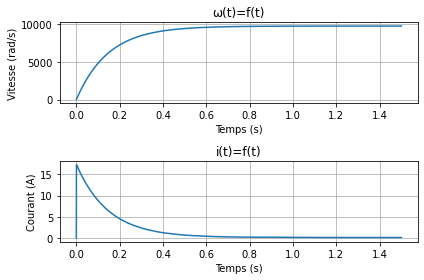
# Tracé de la vitesse
plt.subplot(211)
plt.plot(sol.t, sol.y[0]*30/np.pi, label="ω(t)")
plt.ylabel('Vitesse (rad/s)')
plt.xlabel("Temps (s)")
plt.title("ω(t)=f(t)")
plt.grid(which="both")
# Tracé du courant
plt.subplot(212)
plt.plot(sol.t, sol.y[1], label="i(t)")
plt.ylabel('Courant (A)')
plt.xlabel("Temps (s)")
plt.title("i(t)=f(t)")
plt.grid(which="both")

plt.tight_layout()  # Adaptation de l'affichage pour éviter les superpositions
plt.show()

png

Équations différentielles d'ordre 2¶

Démarche¶

La fonction solve_ivp ne pouvant résoudre que des équations différentielles d'ordre 1, il faut ramener l'équation différentielle d'ordre 2 à un système d'équations différentielles d'ordre 1.

Soit l'équation : $y''(t)+a\, y'(t)+b\,y(t)+c=0$
On pose $y_1(t)=y(t)$ et $y_2(t)=y'(t)$ , ce qui donne : $y_2'(t)+a\, y_1'(t)+b\,y_1(t)+c=0$
On la met sous la forme : $y_2'(t)=-a\, y_1'(t)-b\,y_1(t)-c$
On pose alors le système :

$Y=\left(\begin{array}{l} y_1(t)\\ y_2(t) \end{array}\right)\quad\textrm{et}\quad Y'=\left(\begin{array}{l} y_1'(t)\\ y_2'(t) \end{array}\right)=\left(\begin{array}{c} y_2(t)\\ -a\,y_1'(t)-b\,y_1(t)-c \end{array}\right)$

Cela nous ramène à résoudre le problème de Cauchy suivant :

$\left\{ \begin{array}{l} Y'(t)=\left( \begin{array}{l} y_1'(t)=y_2(t)\\ y_2'(t)=-a\,y_1'(t)-b\,y_1(t)-c \end{array} \right)\\ Y_0=\left[ \begin{array}{l} y_1(t_0)=C_0\\ y_2(t_0)=C_1 \end{array} \right] \end{array} \right.$

Résolution du système :

from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
a = 1
b = 2
c = -1

# Définition des conditions initiales
C_0 = 1
C_1 = 1

# Définition du système d'équation différentielle
def systeme(t, Y, a, b, c):
    y1 = Y[0]
    y2 = Y[1]

    dy1_dt = y2
    dy2_dt = -a*dy1_dt-b*y1-c

    return [dy1_dt, dy2_dt]


# Résolution
solution = solve_ivp(systeme, [0, 1], [C_0, C_1], method='RK45', args=(
    a, b, c))

print(solution.y[0])  # Affichage des valeurs de x1
print(solution.y[1])  # Affichage des valeurs de x2

[1.         1.08294508 1.21527716 1.12981512]
[ 1.          0.81796979 -0.3357434  -0.51734205]

Exemple système masse/ressort¶

Soit le système masse-ressort suivant :

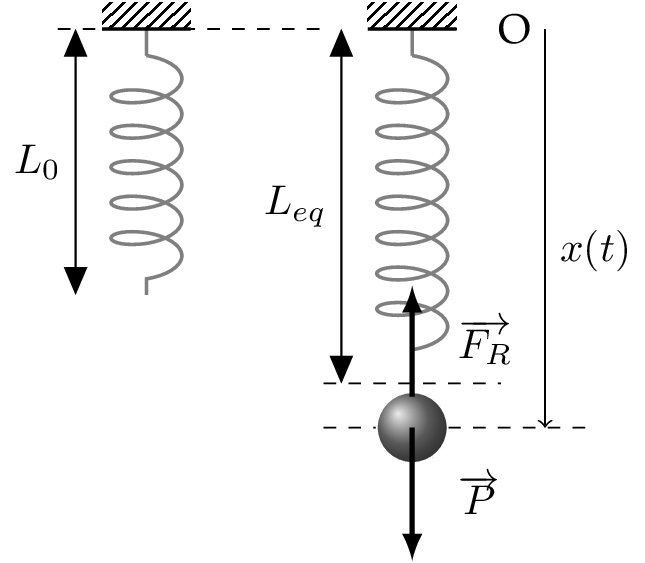
Système masse-ressort

On cherche à connaitre la position de la masse au court du temps en fonction de la position initiale.

En isolant la masse, on identifie 2 efforts qui s'y appliquent dans un modèle simplifié (on prend $\vec{x}$ positif vers le bas) :
- Le poids : $\vec{P}=m\,g\,\vec{x}$
- La force de rappel du ressort : $\vec{F_R}=-k\,(x(t)-L_0)\,\vec{x}$
On ne considère que le déplacement selon l'axe $\vec{x}$ de la masse, elle est donc en translation. En appliquant le principe fondamental de la dynamique, on trouve l'équation : $m\,g\,\vec{x}-k\,(x(t)-L_0)\,\vec{x}=m\,\vec{a}$
La projection sur l'axe $\vec{x}$ nous donne alors l'équation différentielle suivante :

$\ddot{x}(t)=g-(x(t)-L_0)\frac{k}{m}=-\frac{k}{m}x(t)+g+L_0\frac{k}{m}$

En appliquant la méthode précédente et en posant $x(t)=x_1(t)$ et $x_2(t)=\dot{x}(t)$ , on obtient le problème de Cauchy suivant :

$\left\{ \begin{array}{l} X'(t)=\left( \begin{array}{l} x_1'(t)=x_2(t)\\ x_2'(t)=-\frac{k}{m}x_1(t)+g+L_0\frac{k}{m} \end{array} \right)\\ X_0=\left[ \begin{array}{l} x_1(t_0)=C_0\\ x_2(t_0)=C_1 \end{array} \right] \end{array} \right.$

Résolution du système :

#### from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
m = 0.2 # kg
k = 10  # N/m
g = 9.81  # m/s²
L0 = 0.1 # m

# Définition des conditions initiales
C_0 = 0.2  # m
C_1 = 0  # m/s

# Définition du système d'équation différentielle
def systeme(t, X):
    x_1 = X[0]
    x_2 = X[1]

    dx1_dt = x_2
    dx2_dt = -k/m*x_1+g+L0*k/m

    return [dx1_dt, dx2_dt]

t0 = 0 # seconde
tf = 6 # seconde

# Solution exact
w0 = np.sqrt(k/m)
t = np.linspace(t0,tf,100)
masse_x = -(C_0-L0)*np.cos(w0*t)+m*g/k+L0

# Résolution
position = solve_ivp(systeme, [t0, tf], [C_0, C_1], method='RK45',max_step=0.1)

import matplotlib.pyplot as plt

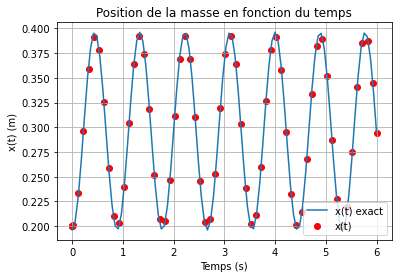
# Tracé de la position de la masse
plt.plot(t, masse_x, label="x(t) exact")
plt.scatter(position.t, position.y[0], label="x(t)", color='red')
plt.ylabel('x(t) (m)')
plt.xlabel("Temps (s)")
plt.title("Position de la masse en fonction du temps")
plt.grid(which="both")
plt.legend()
plt.show()

png

Exemple trajectoire d'un projectile¶

On souhaite connaître la position d'un projectile, dont le système est représenté ci-dessous :

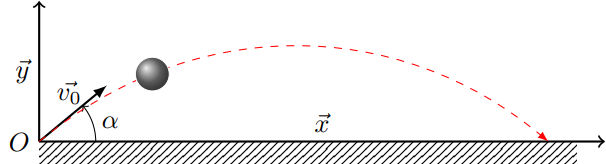
Projectile

On fait les hypothèses suivantes :
- le frottement de l'air est négligeable (vitesse faible de l'objet) : $\vec{f}=\vec{0}$ ;
- la variation de pression atmosphérique négligeable (variation d'altitude faible) : $\vec{F}=\vec{cste}$ ;
- la poussée d'Archimède est négligeable (projectile de densité très supérieure à celle de l'air) : $\vec{F}=\vec{0}$ ;
- l'altitude et la distance parcourue sont très inférieures au rayon de la planète : $\vec{g}=\vec{cste}$ .
Le projectile n'est alors soumis qu'à son poids : $\vec{P}=-m\,\vec{g}$
L'application du principe fondamental de la dynamique, on obtient : $-m\,g\,\vec{y}=m\,\vec{a}$
En projetant sur les deux axes, on obtient le système suivant :

$\left\{\begin{array}{l} \ddot{x}=0\\ \ddot{y}=-g \end{array}\right.$

En posant $X=\dot{x}$ et $Y=\dot{Y}$ , on obtient le système d'équations différentielles suivant :

$\left\{\begin{array}{l} \dot{x}=X\\ \dot{X}=0\\ \dot{y}=Y\\ \dot{Y}=-g \end{array}\right.$

Résolution du système :

from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
m = 1  # kg
g = 9.81  # m/s²

# Définition des conditions initiales
V_0 = 10  # m/s
alpha = 20*np.pi/180  # rad
X_0 = V_0*np.cos(alpha)  # m/s
Y_0 = V_0*np.sin(alpha)  # m/s

x_0 = 0  # m
y_0 = 0  # m

# Définition du système d'équation différentielle
def pos_x(t, Y):
    x = Y[0]
    X = Y[1]
    y = Y[2]
    Y = Y[3]

    dx_dt = X
    dX_dt = 0
    dy_dt = Y
    dY_dt = -g

    return [dx_dt, dX_dt, dy_dt, dY_dt]


# Résolution
position = solve_ivp(
    pos_x, [0, 10], [x_0, X_0, y_0, Y_0], method='RK45', max_step=0.001)

import matplotlib.pyplot as plt
# Recherche de l'index où le projectile est au-dessus du sol
index = np.where(position.y[2] >= 0)  # y>=0

# Tracé de la position du projectile
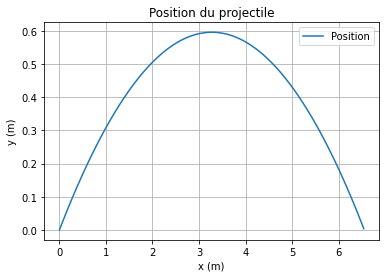
plt.plot(position.y[0][:index[0][-1]], position.y[2]
         [:index[0][-1]], label="Position")
plt.ylabel('y (m)')
plt.xlabel("x (m)")
plt.title("Position du projectile")
plt.grid(which="both")
plt.legend()
# plt.save_fig("projectile.pdf")
plt.show()

png

Équation différentielle d'ordre n¶

Le raisonnement de l'équation différentielle d'ordre 2 peut se généraliser à l'ordre n.

Une équation différentielle d'ordre n peut s'écrire sous la forme d'un système de n équations différentielles d'ordre 1.