Impact des paramètres sur la résolution d'une équation différentielle¶

En fonction des paramètres choisis, les résultats retournés peuvent grandement varier. On va voir ici l'impact de certains paramètres sur les résultats.

Attention

Restez toujours critique vis-à-vis des résultats obtenus. Les outils numériques ne pouvant fournir qu'une approximation de la solution, vous n'avez aucune garantie que le résultat est forcément bon. Pensez à vérifier que les résultats obtenus s'approchent de ce à quoi on s'attend.

Influence de la méthode d'intégration¶

On part sur l'exemple du système masse-ressort dans un modèle simplifié et sur la trajectoire d'un projectile :

L'équation différentielle de la position de la masse vaut : $\ddot{x}=-\frac{k}{m}x$
L'équation temporelle exacte de la position de la masse vaut : $x(t)=x_0\,\cos\left(\sqrt{\frac{k}{m}}\,t\right)$
On garde les mêmes équations pour le projectile.

On compare les résultats pour les méthodes RK23, RK45 et DOP853.

from scipy.integrate import solve_ivp
import numpy as np
from math import sqrt

# Définition des paramètres du système
m = 0.1  # kg
k = 100.  # N/m
w0 = sqrt(k/m)

# Définition des conditions initiales
x_0 = 0.1  # m
X_0 = 0  # m/s

# Définition du système d'équation différentielle
def systeme(t, Y):
    x = Y[0]
    X = Y[1]

    dx_dt = X
    dX_dt = -k/m*x

    return [dx_dt, dX_dt]

# Création des points à calculer
t0 = 0
tf = 10
t = np.linspace(t0,tf,50)

masse_x = x_0*np.cos(w0*t)

# Résolution
masse_rk23 = solve_ivp(systeme,[t0,tf], [x_0, X_0],t_eval=t, method='RK23')
masse_rk45 = solve_ivp(systeme, [t0, tf], [x_0, X_0],t_eval=t, method='RK45')
masse_dop853 = solve_ivp(systeme, [t0, tf], [x_0, X_0],t_eval=t, method='DOP853')

from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
m = 1  # kg
g = 9.81  # m/s²

# Définition des conditions initiales
V_0 = 10  # m/s
alpha = 20*np.pi/180  # rad
X_0 = V_0*np.cos(alpha)  # m/s
Y_0 = V_0*np.sin(alpha)  # m/s

x_0 = 0  # m
y_0 = 0  # m

# Définition du système d'équation différentielle
def pos_x(t, Y):
    x = Y[0]
    X = Y[1]
    y = Y[2]
    Y = Y[3]

    dx_dt = X
    dX_dt = 0
    dy_dt = Y
    dY_dt = -g

    return [dx_dt, dX_dt, dy_dt, dY_dt]

step = 0.1
# Résolution
rk45 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='RK45',max_step = step)
rk23 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='RK23',max_step = step)
dop853 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='DOP853',max_step = step)

import matplotlib.pyplot as plt

# Résultats pour le système masse ressort
plt.subplot(211)
plt.plot(t, masse_x, label="Théorique", marker='+')
plt.plot(masse_rk23.t, masse_rk23.y[0], label="RK23")
plt.plot(masse_rk45.t, masse_rk45.y[0], label="RK45")
plt.plot(masse_dop853.t, masse_dop853.y[0], label="DOP853")
plt.ylabel('x (m)')
plt.xlabel("t (s)")
plt.title("Comparaison des méthodes - Système masse-ressort")
plt.grid(which="both")
plt.legend()

# Résultats pour le projectile
plt.subplot(212)
plt.scatter(rk23.y[0], rk23.y[2], label="RK23", color='red', marker ='x')
plt.plot(rk45.y[0], rk45.y[2], label="RK45")
plt.scatter(dop853.y[0], dop853.y[2], label="DOP853", marker='+', color='yellow')
plt.ylabel('y (m)')
plt.xlabel("x (m)")
plt.title("Comparaison des méthodes - Projectile")
plt.grid(which="both")
plt.legend()

plt.tight_layout()
plt.show()

png

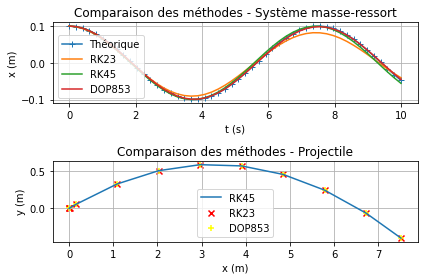
On constate que dans le cas du projectile, les résultats sont sensiblement les mêmes, quelle que soit la méthode utilisée.
Par contre dans le cas du système masse-ressort, on peut voir que la méthode RK23 s'éloigne du résultat attendu progressivement (surement dû à un cumul des erreurs). Les deux autres méthodes semblent plus proches.

import matplotlib.pyplot as plt

# Résultats pour le système masse ressort
plt.plot(t[30:], masse_x[30:], label="Théorique", marker='+')
plt.plot(masse_rk23.t[30:], masse_rk23.y[0][30:], label="RK23")
plt.plot(masse_rk45.t[30:], masse_rk45.y[0][30:], label="RK45")
plt.plot(masse_dop853.t[30:], masse_dop853.y[0][30:], label="DOP853")
plt.ylabel('x (m)')
plt.xlabel("t (s)")
plt.title("Comparaison des méthodes - Système masse-ressort")
plt.grid(which="both")
plt.legend()
plt.show()

png

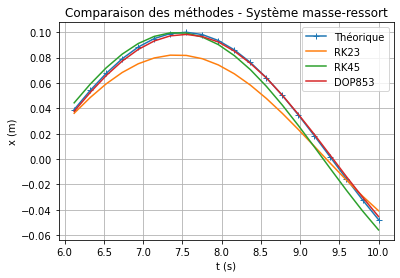
Un zoom sur la dernière partie, nous montre quand même une dérive pour le modèle RK45 par rapport à ce qui est attendu. Ici on pourrait penser que le modèle DOP853 est le plus adapté.

Les autres méthodes¶

Ici on rajoute les autres méthodes pour la comparaison.

from scipy.integrate import solve_ivp
import numpy as np
from math import sqrt

# Définition des paramètres du système
m = 0.1  # kg
k = 100.  # N/m
w0 = sqrt(k/m)

# Définition des conditions initiales
x_0 = 0.1  # m
X_0 = 0  # m/s

# Définition du système d'équation différentielle
def systeme(t, Y):
    x = Y[0]
    X = Y[1]

    dx_dt = X
    dX_dt = -k/m*x

    return [dx_dt, dX_dt]

# Création des points à calculer
t0 = 0
tf = 80
t2 = np.linspace(t0,tf,400)

masse_x = x_0*np.cos(w0*t2)

# Résolution
masse2_radau = solve_ivp(systeme,[t0,tf], [x_0, X_0],t_eval=t2, method='Radau')
masse2_bdf = solve_ivp(systeme,[t0,tf], [x_0, X_0],t_eval=t2, method='BDF')
masse2_lsoda = solve_ivp(systeme,[t0,tf], [x_0, X_0],t_eval=t2, method='LSODA')
masse2_rk45 = solve_ivp(systeme, [t0, tf], [x_0, X_0],t_eval=t2, method='RK45')
masse2_dop853 = solve_ivp(systeme, [t0, tf], [x_0, X_0],t_eval=t2, method='DOP853')

import matplotlib.pyplot as plt

# Résultats pour le système masse ressort
plt.plot(t2[300:], masse_x[300:], label="Théorique", marker='+')
plt.plot(masse2_radau.t[300:], masse2_radau.y[0][300:], label="Radau")
plt.plot(masse2_bdf.t[300:], masse2_bdf.y[0][300:], label="BDF")
plt.plot(masse2_lsoda.t[300:], masse2_lsoda.y[0][300:], label="LSODA")
plt.plot(masse2_rk45.t[300:], masse2_rk45.y[0][300:], label="RK45")
plt.plot(masse2_dop853.t[300:], masse2_dop853.y[0][300:], label="DOP853")
plt.ylabel('x (m)')
plt.xlabel("t (s)")
plt.title("Comparaison des méthodes - Système masse-ressort")
plt.grid(which="both")
plt.legend()
plt.show()

png

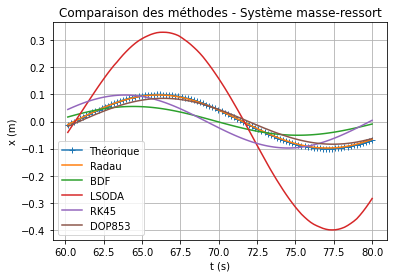
On voit déjà que la méthode LSODA est loin du résultat.

import matplotlib.pyplot as plt

# Résultats pour le système masse ressort
plt.plot(t2[300:], masse_x[300:], label="Théorique", marker='+')
plt.plot(masse2_radau.t[300:], masse2_radau.y[0][300:], label="Radau")
plt.plot(masse2_bdf.t[300:], masse2_bdf.y[0][300:], label="BDF")
plt.plot(masse2_rk45.t[300:], masse2_rk45.y[0][300:], label="RK45")
plt.plot(masse2_dop853.t[300:], masse2_dop853.y[0][300:], label="DOP853")
plt.ylabel('x (m)')
plt.xlabel("t (s)")
plt.title("Comparaison des méthodes - Système masse-ressort")
plt.grid(which="both")
plt.legend()
plt.show()

png

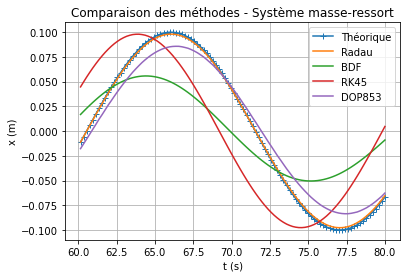
On ne sélectionnant que les méthodes les plus proches, on peut constater que le choix de la méthode DOP853 n'est finalement pas pertinent, car l'amplitude diminue, ce qui n'est presque pas le cas de la méthode RK45. Par contre, cette dernière présente ici un déphasage.

Finalement pour ce cas, la méthode Radau semble la plus précise au niveau des résultats.

Attention

Cette analyse est vraiment pour cette équation différentielle. Elle n'est pas à généraliser pour d'autres types d'équations.
Par exemple, dans le cas du projectile, la méthode RK32 suffit largement.

Influence du pas d'intégration¶

On compare les résultats pour différents pas de calculs.

Cas du projectile¶

from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
m = 1  # kg
g = 9.81  # m/s²

# Définition des conditions initiales
V_0 = 10  # m/s
alpha = 20*np.pi/180  # rad
X_0 = V_0*np.cos(alpha)  # m/s
Y_0 = V_0*np.sin(alpha)  # m/s

x_0 = 0  # m
y_0 = 0  # m

# Définition du système d'équation différentielle
def pos_x(t, Y):
    x = Y[0]
    X = Y[1]
    y = Y[2]
    Y = Y[3]

    dx_dt = X
    dX_dt = 0
    dy_dt = Y
    dY_dt = -g

    return [dx_dt, dX_dt, dy_dt, dY_dt]

step = 0.1
# Résolution
step1 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='RK23',max_step = step)
step = 0.5
step2 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='RK23',max_step = step)
step = 0.3
step3 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='RK23',max_step = step)
step = 0.01
step4 = solve_ivp(
    pos_x, [0, 0.8], [x_0, X_0, y_0, Y_0], method='RK23',max_step = step)

import matplotlib.pyplot as plt

# Résultats pour le projectile
plt.plot(step4.y[0], step4.y[2], label="Pas = 0.01")
plt.scatter(step1.y[0], step1.y[2], label="Pas = 0.1")
plt.scatter(step3.y[0], step3.y[2], label="Pas = 0.3")
plt.scatter(step2.y[0], step2.y[2], label="Pas = 0.5")

plt.ylabel('y (m)')
plt.xlabel("x (m)")
plt.title("Comparaison du pas - Projectile")
plt.grid(which="both")
plt.legend()

plt.tight_layout()
plt.show()

png

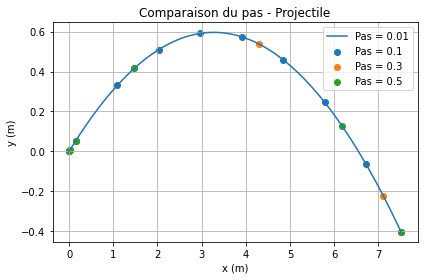
Ici, on voit que le pas ne semble pas avoir d'influence sur la précision du résultat.
Par contre, pour un pas faible, il y a un manque d'information entre deux échantillons qui ne permet pas d'avoir une idée cohérente du comportement du système (voir figure ci-dessous)

Attention

Un pas trop élevé n'est pas toujours souhaitable non plus, car cela va nécessiter beaucoup plus de calcul pour un gain pas forcément appréciable.

import matplotlib.pyplot as plt

# Résultats pour le projectile
plt.plot(step4.y[0], step4.y[2], label="Pas = 0.01")
plt.plot(step1.y[0], step1.y[2], label="Pas = 0.1")
plt.plot(step3.y[0], step3.y[2], label="Pas = 0.3")
plt.plot(step2.y[0], step2.y[2], label="Pas = 0.5")

plt.ylabel('y (m)')
plt.xlabel("x (m)")
plt.title("Comparaison du pas - Projectile")
plt.grid(which="both")
plt.legend()

plt.tight_layout()
plt.show()

png

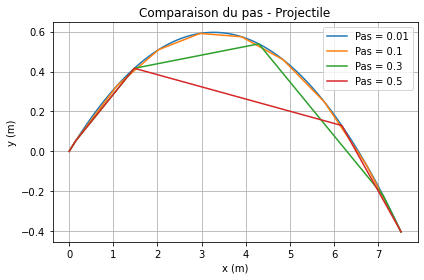
Cas du système masse-ressort¶

from scipy.integrate import solve_ivp
import numpy as np

# Définition des paramètres du système
m = 0.2 # kg
k = 10  # N/m
g = 9.81  # m/s²
L0 = 0.1 # m
w0 = np.sqrt(k/m)

# Définition des conditions initiales
C_0 = 0.2  # m
C_1 = 0  # m/s

# Définition du système d'équation différentielle
def systeme(t, X):
    x_1 = X[0]
    x_2 = X[1]

    dx1_dt = x_2
    dx2_dt = -k/m*x_1+g+L0*k/m

    return [dx1_dt, dx2_dt]

# Création des points à calculer
t0 = 0
tf = 5.
t1 = np.linspace(0,tf,10) # Le pas est définit par le nombre de point à calculer

x1 = -(C_0-L0)*np.cos(w0*t1)+m*g/k+L0

# Résolution
pas1 = solve_ivp(systeme,[t0,tf], [C_0, C_1],t_eval=t1, method='Radau')
t2 = np.linspace(0,tf,25)
pas2 = solve_ivp(systeme, [t0, tf], [C_0, C_1],t_eval=t2, method='Radau')
t3 = np.linspace(0,tf,50)
pas3 = solve_ivp(systeme, [t0, tf], [C_0, C_1],t_eval=t3, method='Radau')
t4 = np.linspace(0,tf,200)
pas4 = solve_ivp(systeme, [t0, tf], [C_0, C_1],t_eval=t4, method='Radau')

import matplotlib.pyplot as plt

# Tracé de la position de la masse
plt.subplot(221)
plt.plot(pas1.t, pas1.y[0])
plt.ylabel('x(t) (m)')
plt.xlabel("Temps (s)")
plt.title("Pas = {}".format(t1[1]))
plt.grid(which="both")
plt.subplot(222)
plt.plot(pas2.t, pas2.y[0])
plt.ylabel('x(t) (m)')
plt.xlabel("Temps (s)")
plt.title("Pas = {}".format(t2[1]))
plt.grid(which="both")
plt.subplot(223)
plt.plot(pas3.t, pas3.y[0])
plt.ylabel('x(t) (m)')
plt.xlabel("Temps (s)")
plt.title("Pas = {}".format(t3[1]))
plt.grid(which="both")
plt.subplot(224)
plt.plot(pas4.t, pas4.y[0])
plt.ylabel('x(t) (m)')
plt.xlabel("Temps (s)")
plt.title("Pas = {}".format(t4[1]))
plt.grid(which="both")

plt.tight_layout()
plt.show()

png

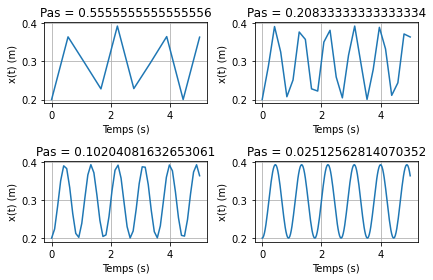
On observe le même phénomène. Si le pas est trop grand, on manque d'information pour connaître exactement le comportement du système.