Dichotomie¶

La méthode de recherche par dichotomie permet d'approche la solution d'une fonction $f(x)=0$ .

Principe de la méthode¶

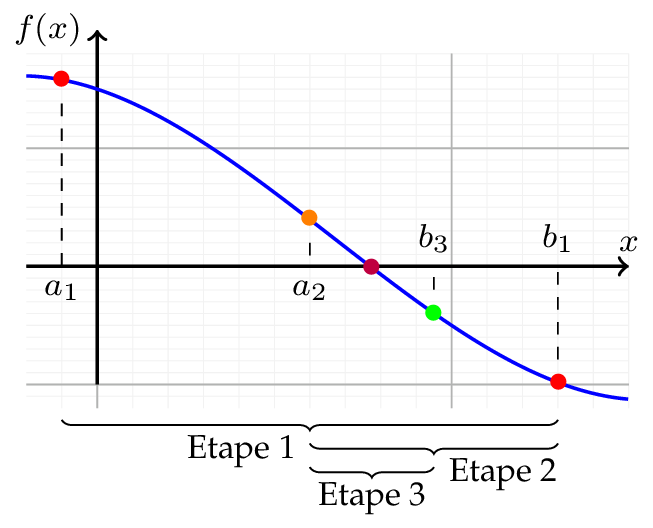
Soit deux valeurs a et b et la fonction $f(x)=0$ continue sur l'intervalle [a,b].
L'encadrement par a et b est tel que $f(a)$ et $f(b)$ sont de signes opposés.
Pour trouver la solution, on divise l'intervalle en deux parties égales avec comme milieu $m=\frac{a+b}{2}$ . Si $f(a)\times f(m)$ sont de même signe, la solution se trouve alors dans l'encadrement [m,b] sinon elle se trouve dans l'encadrement [a,m].
On réitère alors la recherche dans le nouveau l'encadrement jusqu'à ce que $a-b$ soit inférieur à la précision voulue.

Dichotomie

Écriture de l'algorithme¶

def dichotomie(f, a, b, epsilon):
    try:
        if f(a)*f(b) > 0:  # On vérifie l'encadrement de la fonction
            raise Exception("Mauvais choix de a ou b.")
        else:
            m = (a + b)/2.
            while abs(a - b) > epsilon:
                if f(m) == 0.:
                    return m
                elif f(a)*f(m) > 0:
                    a = m
                else:
                    b = m
                m = (a + b)/2
            return m
    except:
        print("Mauvais choix de l'encadrement")
        return 0

Exemple¶

On cherche à résoudre $f(x)=0$ avec : $f(x)=5x^2+2x-34$

On définit la fonction f(x)$ dans python.

def f(x):
    return 5*x**2+2*x-34

Ci-dessous le tracé de la fonction $f(x)$ .

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-4, 4, 100)

plt.plot(x, f(x))
plt.axhline(y=0, color="black")
plt.axvline(x=0, color="black")
plt.grid(True)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("Tracé de f(x)")
plt.show()

png

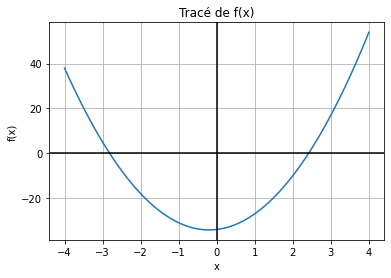
On peut voir sur le graphe que la fonction admet deux solutions.
On va alors chercher les solutions dans les deux intervalles [-4,-1] et [1,4] en utilisant la méthode de recherche par dichotomie.

x1 = dichotomie(f, -4, -1, 0.001)
x2 = dichotomie(f, 1, 4, 0.001)

print(x1, x2)

1	`-2.8153076171875 2.4154052734375`

Tracer l'évolution d'une fonction f(x,z)=0¶

Il arrive de devoir tracer l'évolution d'une fonction qui contient deux variables selon une équation $f(x,z)=0$ .
Si l'on connait l'évolution d'une des deux variables, il est alors possible de calculer les solutions de la fonction par la méthode de recherche par dichotomie.

Exemple avec une loi E/S géométrique¶

Exemple d'équation de loi E/S géométrique pour un système de moteur à piston d'équation $f(x(t),\alpha(t))=0$ avec

$f(x(t),\alpha(t))=-b^2+L^2+a^2+x(t)^2-2\left[x(t).L+(a.L-a.x(t))\cos(\alpha(t))\right]$

On souhaite tracer $x(t)=f(\alpha)$ .

Résolution numérique¶

La fonction dichotomie a été modifiée pour pouvoir passer la seconde variable de la fonction $f(x,\alpha)=0$ .

import matplotlib.pyplot as plt
import numpy as np


def dichotomie(f, alpha, a, b, epsilon):
    try:
        if f(a, alpha)*f(b, alpha) > 0:  # On vérifie l'encadrement de la fonction
            raise Exception("Mauvais choix de a et b.")
        else:
           # a, b = min(a, b), max(a, b)
            m = (a + b)/2.
            while abs(a - b) > epsilon:
                if f(m, alpha) == 0.:
                    return m
                elif f(a, alpha)*f(m, alpha) > 0:
                    a = m
                else:
                    b = m
                m = (a + b)/2
            return m
    except:
        print("Mauvais choix de l'encadrement")
        return 0


# Fonction f(x,alpha)=0
def f(x, alpha):
    # Grandeurs fixes du problème
    a = 9e-3  # mm
    b = 4e-2  # mm
    L = a+b
    return L**2+a**2+x**2-2*(x*L+(a*L-a*x)*np.cos(alpha))-b**2


# alpha fait un tour complet
alpha = np.linspace(0, 2*np.pi, 100)
x = []

# Recherche de chaque valeur de x pour chaque valeur de alpha
for z in alpha:
    x.append(dichotomie(f, z, 0, 2.1*9e-3, 0.0001))

# Tracé de la solution
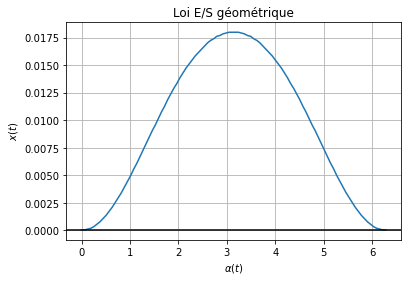
plt.plot(alpha, x)
plt.axhline(y=0, color="black")
plt.xlabel(r'$\alpha(t)$')
plt.ylabel(r'$x(t)$')
plt.title("Loi E/S géométrique")
plt.grid()
plt.show()

png