Modélisation et réponse des SLCI¶

Le module scipy.signal permet un certain nombre de traitements, calcul, modélisation autour des systèmes linéaire, continu et invariant (SLCI).

Pour cette partie, nous nous baserons sur le modèle d'une machine à courant continu dont le schéma-bloc et visible ci-dessous :

MCC

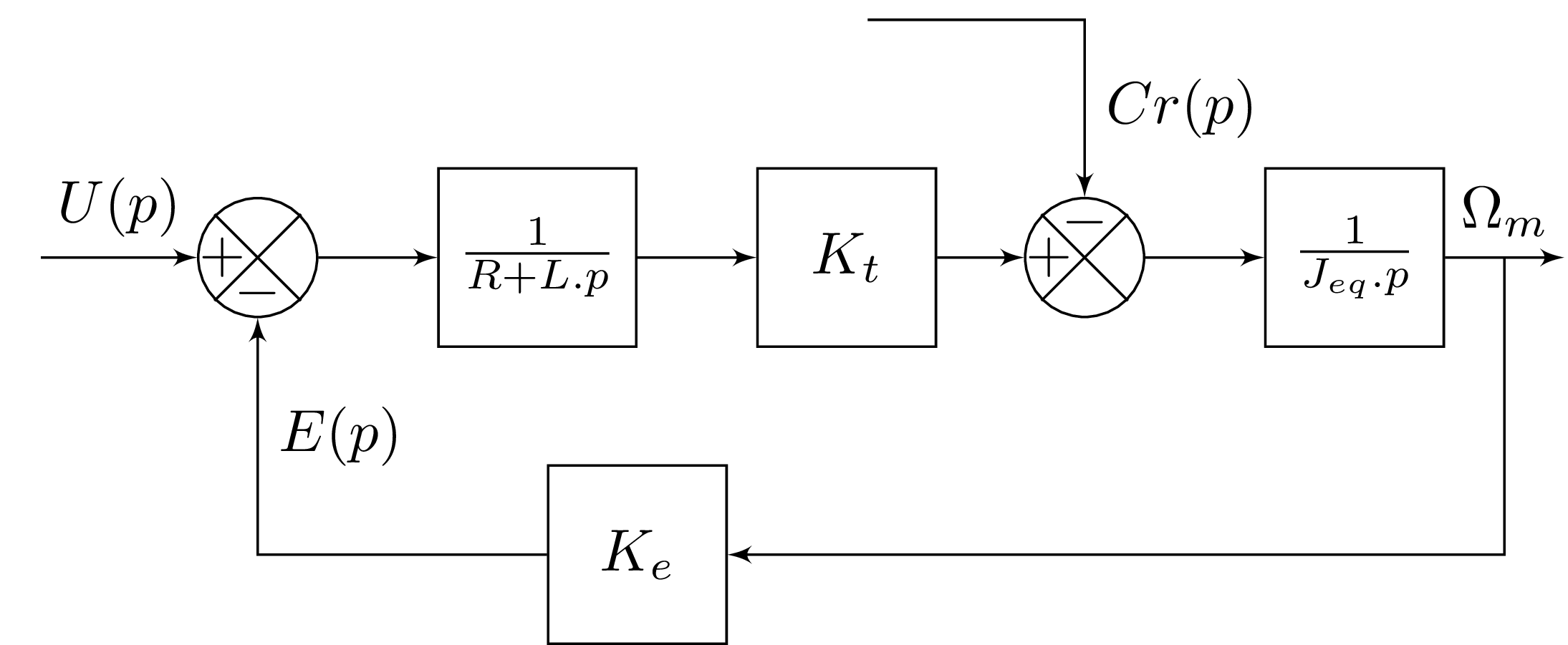
Avec les grandeurs physiques suivantes :

Tension nominale : 12 V
Résistance d'induit : 2,07 $\Omega$
Inductance d'induit : 0,227 mH
Constante de couple : 13,9 mNm/A
Constante de vitesse : 689 rmp/V
Couple résistant (frottement sec ici) : 0,7923 mNm
Inertie du rotor : 13,6 gcm²

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Constantes du système

Un = 12  # V
R = 2.07  # Ohms
L = 0.227e-3  # H
Kt = 13.9e-3  # Nm/A
Ke = 1/(np.pi*689/30)
Cr = 0.7923e-3  # Nm
Jeq = 13.6e-7  # kgm²

Modélisation du système¶

Pour construire un modèle SLCI sous python, il existe la fonction signal.lti() qui permet de créer le système SLCI.

Le système peut être créé de 3 façons différentes :

Par la fonction de transfert en passant le numérateur et le dénominateur comme paramètres ;
Par la connaissance des zéros, pôles et gains du système ;
Par une représentation d'états avec comme paramètres A, B, C, D.

Plus d'information à la page scipy.signal.lti

Info

Dans notre cas, nous utiliserons uniquement les fonctions de transfert, en appelant la fonction par signal.lti(num,denom) avec num et denom des tableaux du numérateur et du dénominateur de la fonction de transfert.
Par exemple pour $H(p)=\frac{2p+1}{5+3p+p^2}$ , on aura num = [2,1] et denom = [1,3,5]. S’il n'y a pas de dénominateur, denom = [1].

Démarche¶

Dans le cas de la MCC, nous avons un système à deux entrées $U(p)$ et $Cr(p)$ qui est impossible à définir directement dans python.

Il faudra utiliser le théorème de superposition pour calculer la réponse complète du système avec deux fonctions de transfert :

$H_U(p) = \frac{\Omega_m(p)}{U(p)}$ avec $Cr(p)=0$ ;
$H_{Cr}(p) = \frac{\Omega_m(p)}{Cr(p)}$ avec $U(p)=0$ .

Fonction de transfert sans perturbation¶

Dans un premier temps, nous n'allons pas tenir compte de la perturbation ( $Cr=0$ ).

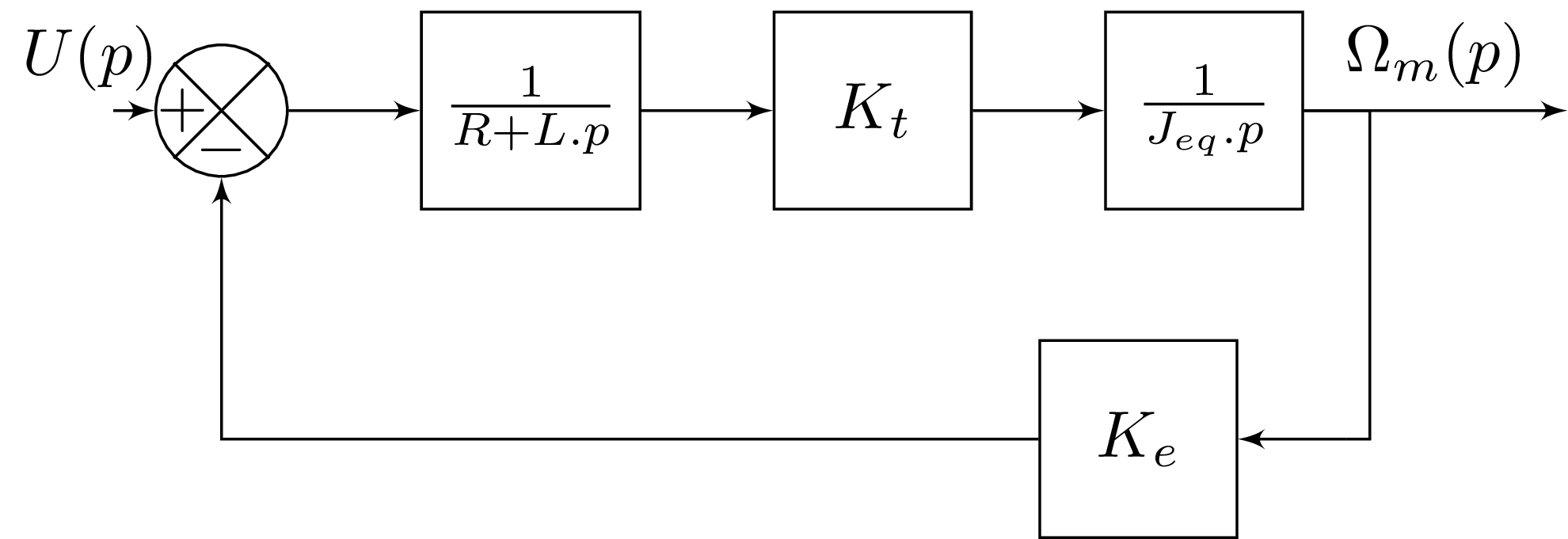
MCC Cr=0

La fonction de transfert vos : $H_U(p)=\frac{\frac{1}{R+Lp}K_t\frac{1}{J_{eq}p}}{1+\frac{1}{R+Lp}K_t\frac{1}{J_{eq}p}K_e}$

Une fois mise sous forme canonique, on obtient :

$H_U(p)=\frac{\frac{1}{K_e}}{1+\frac{R.J_{eq}}{K_e.K_t}p+\frac{L.J_{eq}}{K_e.K_t}p^2}$

# Construction du modèle

# Définition du numérateur et du dénominateur
num = [1/Ke]
denom = [L*Jeq/(Ke*Kt), R*Jeq/(Ke*Kt), 1]

# Création de la fonction de transfert
ft_U = signal.lti(num, denom)

Fonction de transfert de la perturbation¶

Si on pose $U(p)=0$ , on obtient le modèle suivant :

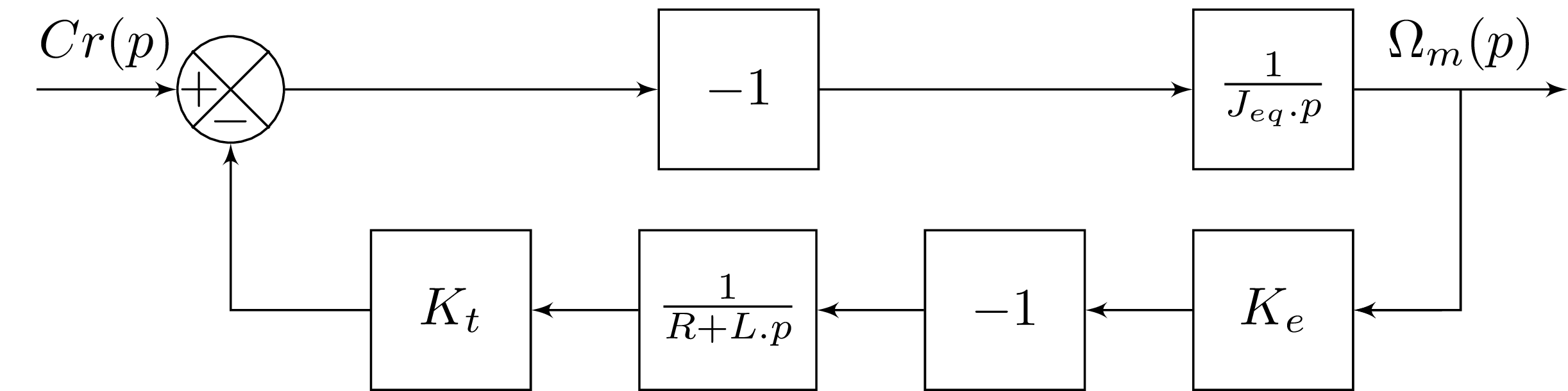
Mcc U=0

La fonction de transfert sous forme canonique vaut alors :

$H_{Cr}(p)=\frac{-\frac{R}{K_e.K_t}-\frac{L}{K_e.K_t}p}{1+\frac{R.J_{eq}}{K_e.K_t}p+\frac{L.J_{eq}}{K_e.K_t}p^2}$

# Construction du modèle

# Définition du numérateur et du dénominateur
num = [-L/(Ke*Kt), -R/(Ke*Kt)]
denom = [L*Jeq/(Ke*Kt), R*Jeq/(Ke*Kt), 1]

# Création de la fonction de transfert
ft_Cr = signal.lti(num, denom)

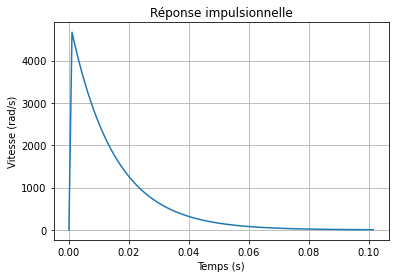
Réponse impulsionnelle¶

Calcul de la réponse impulsionnelle sans perturbation.

Pour cela on utilise la fonction signal.impulse(ft, X0=None, T=None, N=None) avec comme paramètres optionnels :

X0 le vecteur d'état initial, par défaut nul ;
T un tableau des instants temporel à calculer ;
N le nombre de points à calculer si T n'est pas défini.

# Réponse impulsionnelle
t, y = signal.impulse(ft_U, N=100)

# Affichage

plt.plot(t, y)
plt.grid(True)
plt.xlabel("Temps (s)")
plt.ylabel("Vitesse (rad/s)")
plt.title("Réponse impulsionnelle")
plt.show()

png

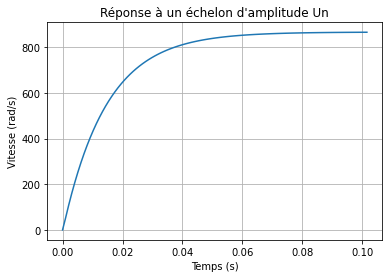
Réponse indicielle ou réponse à un échelon¶

Calcul de la réponse à un échelon unitaire sans perturbation.

La fonction utilisée est signal.step(ft, X0=None, T=None, N=None) avec comme paramètres optionnels :

X0 le vecteur d'état initial, par défaut nul ;
T un tableau des instants temporel à calculer ;
N le nombre de points à calculer si T n'est as défini.

La fonction calcul la réponse à un échelon unitaire uniquement. Pour d'autres valeurs d'échelon, il suffit de multiplier la réponse l'amplitude de l'échelon.

# Réponse indicielle
t, y = signal.step(ft_U)

# La tension appliquée étant de Un=12 V pour le moteur
y = y*Un

# Affichage
plt.plot(t, y)
plt.grid(True)
plt.xlabel("Temps (s)")
plt.ylabel("Vitesse (rad/s)")
plt.title("Réponse à un échelon d'amplitude Un")
plt.show()

print("Valeur finale (tr/min) :", y[-1]*30/np.pi)

png

1	`Valeur finale (tr/min) : 8260.402674813595`

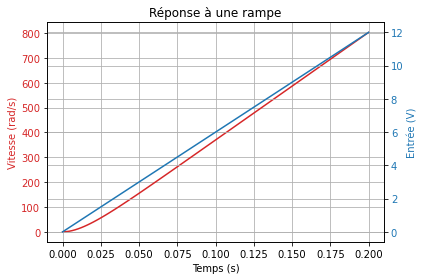
Réponse à une entrée quelconque¶

Il est possible de calculer la réponse du système pour n'importe quelle entrée avec la fonction signal.lsim(ft, U, T, X0=None) avec les paramètres suivants :

U un tableau de l'amplitude de l'entrée ;
T un tableau des instants temporels de calcul de même taille que U ;
X0 un vecteur d'état initial, par défaut nul .

# Construction de l'entrée
temps = np.linspace(0, 0.2, 100)
entree = np.linspace(0, Un, 100)  # Une rampe

t, y, _ = signal.lsim(ft_U, U=entree, T=temps)

fig, ax1 = plt.subplots()

color = 'tab:red'
ax1.set_xlabel('Temps (s)')
ax1.set_ylabel('Vitesse (rad/s)', color=color)
ax1.plot(t, y, color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax1.grid(True)

ax2 = ax1.twinx()  # Création d'un deuxième axe qui partage le même axe x

color = 'tab:blue'
ax2.set_ylabel('Entrée (V)', color=color)  # Label de l'axe x
ax2.plot(temps, entree, color=color)
ax2.tick_params(axis='y', labelcolor=color)

plt.grid(True)
plt.title("Réponse à une rampe")
fig.tight_layout()  # Amélioration de l'affichage
plt.show()

png

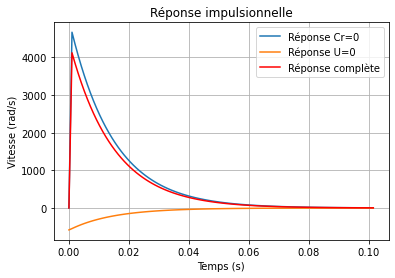
Réponse avec la perturbation¶

Cette fois on va calculer la réponse en tenant compte de la perturbation en utilisant le théorème de superposition.

Attention

Le couple résistant étant un couple de frottement, il ne fera pas tourner le moteur en sens inverse, il faut donc "supprimer" les valeurs négatives qui seront calculées par le théorème de superposition.

Réponse impulsionnelle¶

# Réponse impulsionnelle
t_U, y_U = signal.impulse(ft_U, N=100)  # Sans perturbation
t_Cr, y_Cr = signal.impulse(ft_Cr, N=100)  # De la perturbation

y_Cr = y_Cr*Cr  # Application du couple résistant

y = y_U+y_Cr  # Calcul de la réponse complète
y[np.where(y < 0)] = 0  # Pas de valeurs négatives ici pour le moteur

# Affichage

plt.plot(t_U, y_U, label="Réponse Cr=0")
plt.plot(t_Cr, y_Cr, label="Réponse U=0")
plt.plot(t_U, y, label="Réponse complète", color="red")
plt.grid(True)
plt.legend()
plt.xlabel("Temps (s)")
plt.ylabel("Vitesse (rad/s)")
plt.title("Réponse impulsionnelle")
plt.show()

png

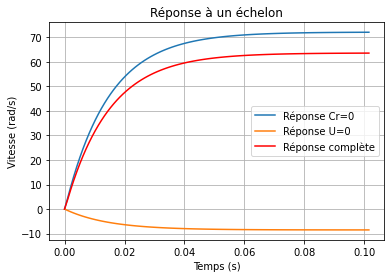
Réponse à un échelon¶

# Réponse impulsionnelle unitaire
t_U, y_U = signal.step(ft_U, N=100)  # Sans perturbation
t_Cr, y_Cr = signal.step(ft_Cr, N=100)  # De la perturbation

y_Cr = y_Cr*Cr  # Application du couple résistant

y = y_U+y_Cr  # Calcul de la réponse complète
y[np.where(y < 0)] = 0  # Pas de valeurs négatives ici pour le moteur

# Affichage

plt.plot(t_U, y_U, label="Réponse Cr=0")
plt.plot(t_Cr, y_Cr, label="Réponse U=0")
plt.plot(t_U, y, label="Réponse complète", color="red")
plt.grid(True)
plt.legend()
plt.xlabel("Temps (s)")
plt.ylabel("Vitesse (rad/s)")
plt.title("Réponse à un échelon")
plt.show()

png