Tracer les diagrammes de Bode¶

Attention

Comme pour la modélisation des SLCI, nous ne travaillerons qu'avec les fonctions de transfert.

Pour calculer les éléments du diagramme de Bode, nous utiliserons la fonction signal.bode(ft, w=None, n=100) avec :

ft la fonction de transfert ;
w un tableau des pulsations à calculer ;
n nombre de pulsations à calculer si w n'est pas défini.

Exemple pour une MCC avec un modèle d'ordre 1¶

Soit la fonction de transfert simplifier de la MCC suivante :

$H_\Omega(p)=\frac{\frac{1}{Ke}}{\frac{R.Jeq}{Ke.Kt}p+1}$

Avec :

Résistance d'induit : 2,07 $\Omega$
Constante de couple : 13,9 mNm/A
Constante de vitesse : 689 rmp/V
Inertie du rotor : 13,6 gcm²

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Constantes du système

R = 2.07  # Ohms
Kt = 13.9e-3  # Nm/A
Ke = 1/(np.pi*689/30)
Jeq = 13.6e-7  # kgm²

# Modélisation de la fonction de transfert
ft = signal.lti([1/Ke], [R*Jeq/(Ke*Kt), 1])

# Calcul du diagramme de Bode
omega = np.logspace(0.8, 3.4, 1000)
w, mag, phase = signal.bode(ft, w=omega)


# Affichage
plt.subplot(211)
plt.title('Diagrammes de Bode')
plt.semilogx(w, mag, lw=2)    # Amplitude
#plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Amplitude (dB)')
plt.grid(which='both')

plt.subplot(212)
plt.semilogx(w, phase)  # Phase
plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Phase (deg)')
plt.grid(which='both')

plt.tight_layout()  # Ajuster le placement des courbes
plt.show()

png

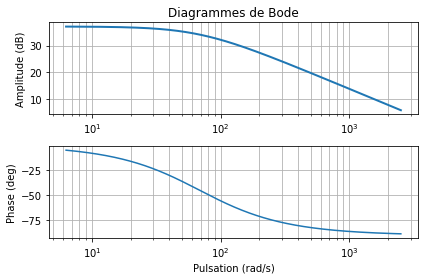
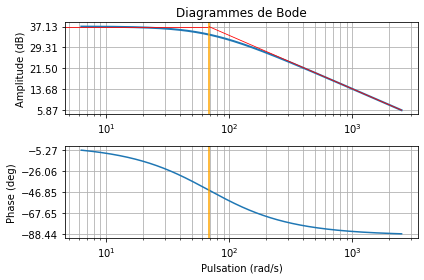
Recherche des éléments caractéristiques¶

# Calcul des éléments caractéristiques de la fonction
# Pente finale
# On cherche les valeurs de la dernière décade
amp = mag[np.where(w >= w[-1]/10)]
print("Pente en dB :", amp[-1]-amp[0])  # Afichage de la pente en dB

# Pulsation de coupure
wc = w[np.where(mag <= mag[0]-3)][0]
print("Pulsation de coupure (rad/s):", wc)

# Calcul de l'asymptote
# Pente avec omega en échelle logarithmique
a = (mag[-2]-mag[-1])/(np.log(w[-2])-np.log(w[-1]))
# Pulsation de coupure en échelle logarithmique
x1 = np.log(w[-1])  # Recherche de la valeur de la pulsation de coupure
b = mag[-1]-a*x1
# Valeurs de la tangente
asymp = a*np.log(w)+b
# On limite les valeurs à partir de la pulsation de coupure
asymp = asymp[np.where(mag <= mag[0]-3)]
omega_t = w[np.where(mag <= mag[0]-3)]


# Affichage
fig, ax = plt.subplots()
plt.subplot(211)
plt.title('Diagrammes de Bode')
plt.semilogx(w, mag, lw=2)    # Amplitude
plt.plot([0, wc], [mag[0], mag[0]], color="red",
         lw=0.8)  # Asymptote horizontale
plt.axvline(x=wc, color="orange")
plt.plot(omega_t, asymp, color="red", lw=0.8)  # Asymptote oblique
#plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Amplitude (dB)')
# On force l'affichage des valeurs extrèmes
plt.yticks(np.linspace(mag[0], mag[-1], 5))
plt.grid(which='both')

plt.subplot(212)
plt.semilogx(w, phase)  # Phase
plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Phase (deg)')
plt.yticks(np.linspace(phase[0], phase[-1], 5))  # On force l'affichage de -90
plt.axvline(x=wc, color="orange")  # Pulsation de coupure
plt.grid(which='both')

plt.tight_layout()  # Ajuster le placement des courbes
plt.show()

Pente en dB : -19.681110428147157
Pulsation de coupure (rad/s): 68.93478706783507

png

Exemple pour une MCC avec un modèle d'ordre 2¶

Soit la fonction de transfert de la MCC suivante :

$H_\Omega(p)=\frac{\frac{1}{Ke}}{\frac{L.Jeq}{Ke.Kt}p^2+\frac{R.Jeq}{Ke.Kt}p+1}$

Avec :

Résistance d'induit : 2,07 $\Omega$
Inductance d'induit : 0,227 mH
Constante de couple : 13,9 mNm/A
Constante de vitesse : 689 rmp/V
Inertie du rotor : 13,6 gcm²

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Constantes du système

Un = 12  # V
R = 2.07  # Ohms
L = 0.227e-3  # H
Kt = 13.9e-3  # Nm/A
Ke = 1/(np.pi*689/30)
Jeq = 13.6e-7  # kgm²

# Construction du modèle

# Définition du numérateur et du dénominateur
num = [1/Ke]
denom = [L*Jeq/(Ke*Kt), R*Jeq/(Ke*Kt), 1]

# Création de la fonction de transfert
ft = signal.lti(num, denom)

# Calcul du diagramme de Bode
omega = np.logspace(0.5, 6, 1000)
w, mag, phase = signal.bode(ft, w=omega)


# Affichage
plt.subplot(211)
plt.title('Diagrammes de Bode')
plt.semilogx(w, mag, lw=2)    # Amplitude
plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Amplitude (dB)')
plt.grid(which='both')

plt.subplot(212)
plt.semilogx(w, phase)  # Phase
plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Phase (deg)')
plt.grid(which='both')

plt.tight_layout()  # Ajuster le placement des courbes
plt.show()

png

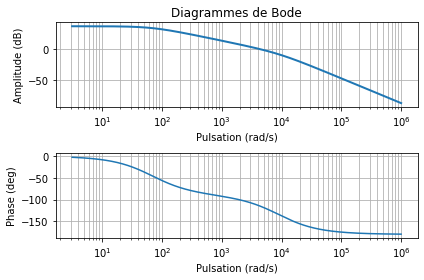
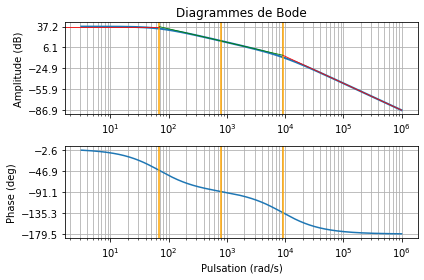
Recherche des grandeurs caractéristiques¶

# Calcul des éléments caractéristiques de la fonction
# Pente finale
# On cherche les valeurs de la dernière décade
amp = mag[np.where(w >= w[-1]/10)]
print("Pente en dB :", amp[-1]-amp[0])  # Afichage de la pente en dB

# Calcul de l'asymptote à -40dB/deca
# Pente avec omega en échelle logarithmique
a = (mag[-2]-mag[-1])/(np.log(w[-2])-np.log(w[-1]))
# Pulsation de coupure en échelle logarithmique
x1 = np.log(w[-1])  # Recherche de la valeur de la pulsation de coupure
b = mag[-1]-a*x1
# Valeurs de l'asymptote
asymp = a*np.log(w)+b

# Pulsation de coupure
wc = w[np.where(asymp <= mag[0])][0]
print("Pulsation de coupure (rad/s):", wc)

# Calcul de l'asymptote à -20dB/dec
a2 = -20/np.log(10)
b2 = mag[np.where(w == wc)][0]-a2*np.log(wc)
asymp2 = a2*np.log(w)+b2

# pulsations caractéristiques
w1 = w[np.where(asymp2 <= mag[0])][0]
w2 = w[np.where(asymp <= asymp2)][0]
print("Pulsation omega 1 :", w1)
print("Pulsation omega 2 :", w2)

# On limite les valeurs à partir de la pulsation de coupure
index_w1 = np.where(w >= w1)[0][0]  # Index de la pulsation omega 1
index_w2 = np.where(w >= w2)[0][0]  # index de la pulsation omega2

asymp = asymp[index_w2:]
omega_t = w[index_w2:]
asymp2 = asymp2[index_w1:index_w2]
omega_t2 = w[index_w1:index_w2]

# Affichage
plt.subplot(211)
plt.title('Diagrammes de Bode')
plt.semilogx(w, mag, lw=2)    # Amplitude

# Pulsations
plt.axvline(x=wc, color="orange")
plt.axvline(x=w1, color="orange")
plt.axvline(x=w2, color="orange")

# Asymptotes
plt.plot([0, w1], [mag[0], mag[0]], color="red",
         lw=0.8)  # Asymptote horizontale
plt.plot(omega_t, asymp, color="red", lw=0.8)  # Asymptote oblique -40dB/dec
# Asymptote oblique -20dB/dec
plt.plot(omega_t2, asymp2, color="green", lw=0.8)

#plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Amplitude (dB)')
# On force l'affichage des valeurs extrèmes
plt.yticks(np.linspace(mag[0], mag[-1], 5))
plt.grid(which='both')

plt.subplot(212)
plt.semilogx(w, phase)  # Phase
plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Phase (deg)')
plt.grid(which='both')
# On force l'affichage des valeurs extrêmes
plt.yticks(np.linspace(phase[0], phase[-1], 5))

# Pulsations
plt.axvline(x=wc, color="orange")
plt.axvline(x=w1, color="orange")
plt.axvline(x=w2, color="orange")

plt.tight_layout()  # Ajuster le placement des courbes
plt.show()

Pente en dB : -39.82535337832185
Pulsation de coupure (rad/s): 795.0609080952509
Pulsation omega 1 : 68.83952069645497
Pulsation omega 2 : 9182.542835656282

png

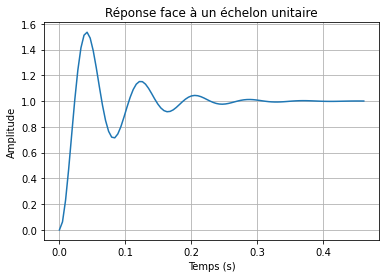
Fonction de transfert d'ordre 2 avec dépassement¶

On prendra pour l'exemple la boucle de position suivante :

Boucle position

Avec $H_{\Omega}(p)=\frac{1}{1+\tau p}$ ou $\tau=33$ ms.

La fonction de transfert $H_\theta(p)$ vaut alors :

$H_\theta(p) = \frac{1}{1+\frac{p}{K_1}+\frac{\tau}{K_1}p^2}$

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

tau = 33e-3  # s
K1 = 200

# Fonction de transfert
ft = signal.lti([1], [tau/K1, 1/K1, 1])

# Calcul de la réponse face à un échelon
T, y = signal.step(ft)

# Affichage de la réponse
plt.plot(T, y)
plt.title("Réponse face à un échelon unitaire")
plt.xlabel('Temps (s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.show()

png

# Calcul du diagramme de Bode
freq = np.logspace(0.5, 3, num=100)
w, mag, phase = signal.bode(ft, w=freq)

# Affichage du diagramme de Bode

plt.subplot(211)
plt.title('Diagramme de Bode')
plt.semilogx(w, mag)    # Bode magnitude plot
#plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Amplitude (dB)')
plt.grid(which='both')
# On force l'affichage des valeurs extrèmes
plt.yticks(np.linspace(mag[0], mag[-1], 5))

plt.subplot(212)
plt.semilogx(w, phase)  # Bode phase plot
plt.xlabel('Pulsation (rad/s)')
plt.ylabel('Phase (deg)')
plt.grid(which='both')
# On force l'affichage des valeurs extrêmes
plt.yticks(np.linspace(phase[0], phase[-1], 5))

plt.tight_layout()  # Ajuster le placement des courbes
plt.show()

png

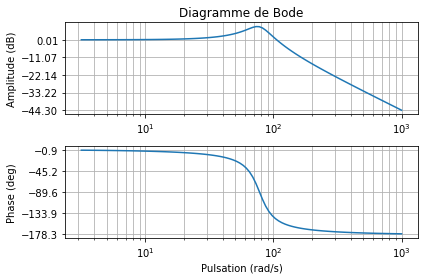
Recherche des grandeurs caractéristiques¶

# Calcul des éléments caractéristiques de la fonction
# Pente finale
# On cherche les valeurs de la dernière décade
amp = mag[np.where(w >= w[-1]/10)]
print("Pente en dB :", amp[-1]-amp[0])  # Afichage de la pente en dB

# Valeur maximale
mag_max = np.max(mag)
ind_max = np.argmax(mag)
print("Amplitude max en dB :", mag_max)


# Calcul de l'asymptote à -40dB/deca
# Pente avec omega en échelle logarithmique
a = (mag[-2]-mag[-1])/(np.log(w[-2])-np.log(w[-1]))
# Pulsation de coupure en échelle logarithmique
x1 = np.log(w[-1])  # Recherche de la valeur de la pulsation de coupure
b = mag[-1]-a*x1
# Valeurs de l'asymptote
asymp = a*np.log(w)+b

# Pulsation de coupure
wc = w[np.where(asymp <= mag[0])][0]
print("Pulsation de coupure (rad/s):", wc)

# Pulsation de résonnance
wr = w[ind_max]
print("Pulsation de résonnance (rad/s):", wr)

Pente en dB : -44.95694559048578
Amplitude max en dB : 8.306650839958799
Pulsation de coupure (rad/s): 82.0618709130545
Pulsation de résonnance (rad/s): 73.05271542664453