Identification des paramètres d'un système d'ordre 1 et 2¶
Trouver les paramètres d'un système à partir des mesures effectuées sur ce dernier pour une entrée de type échelon. La réponse est de la forme d'un premier ordre ou d'un second ordre.
Pour cela, nous allons utiliser NumPy pour l'identification et SciPy pour valider le modèle.
Système d'ordre 1¶
Les données mesurées sont stockées dans le fichier "Ordre1.csv".
Lecture des données¶
import numpy as np
# Lecture des en-têtes des données avec comme délimiteur le point-virgule
head = np.loadtxt('Ordre1.csv', delimiter=';', max_rows=1, dtype=np.str)
# Lecture des données au format str
data = np.loadtxt('Ordre1.csv', delimiter=';', skiprows=1, dtype=np.str)
# Affichage des en-têtes
print(head)
# Sélections des données en fonction de l'en-tête et conversion en flottant
temps = np.asarray(data[:, 2], dtype=np.float, order='C').flatten()
mesure = np.asarray(data[:, 5], dtype=np.float, order='C').flatten()
1 2 3 | |
import matplotlib.pyplot as plt # Module pour tracer les graphiques
# Ajout du d'une courbe avec label
plt.plot(temps, mesure, label="Vitesse (rpm)")
plt.ylabel('Vitesse (rpm)') # Titre de l'axe y
plt.xlabel("Temps (ms)") # Titre de l'axe x
plt.title("Mesure brut") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.show() # Affichage d'une courbe
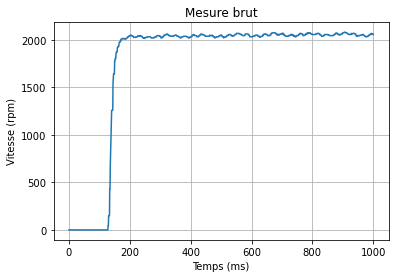
Identification début et fin de la réponse¶
Le signal mesuré oscillant légèrement une fois la valeur finale atteinte, un filtrage est nécessaire pour éliminer ces oscillations.
from scipy import signal
# Fréquence d'échantillonnage
fe = 1000/(temps[1]-temps[0]) # Hz
# Fréquence de nyquist
f_nyq = fe / 2. # Hz
# Fréquence de coupure à adapter
fc = 90 # Hz
# Préparation du filtre de Butterworth en passe-bas
b, a = signal.butter(4, fc/f_nyq, 'low', analog=False)
# Application du filtre
mesureF = signal.filtfilt(b, a, mesure)
Dans un premier temps on élimine les données inutiles (zone morte avant le début de l'action, temps d'acquisition trop long).
L'objectif est de trouver le début et la fin de la réponse du système.
# Recherche du début et de la fin en fonction de l'amplitude de la différence de la courbe
diff_mesure = np.diff(mesureF)
# La valeur de test est à adapter en fonction des cas
dt = np.where(diff_mesure > 5)
print(dt)
debut = dt[0][0] # Premier élement de l'intervalle
fin = dt[0][-1] # Dernier élément de l'intervalle
# Affichage
plt.ylabel('Vitesse (rpm)') # Titre de l'axe y
plt.xlabel("Indice") # Titre de l'axe x
plt.title("Validation des intervalles") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.plot(mesure[debut:fin])
plt.show()
1 2 3 4 | |
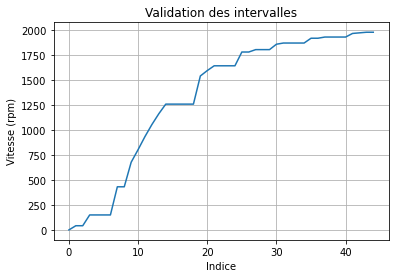
Recherche des éléments caractéristiques de la réponse¶
On cherche les éléments caractéristiques des signaux :
E0consigne de l'échelon (imposé dans cet essai)Sinfvaleur finale de la mesureGgain statique de la réponse
# Calcul de la valeur final
Sinf = np.mean(mesure[fin:])
print("Valeur finale (rpm) :", Sinf)
# Recherche du gain
E0 = 20.77*0.2 # V, Ici on a une tension d'alimentation de 20,77 V avec une consigne de 20 %
print("Entrée (V) :", E0)
G = Sinf/E0
print('Gain (rpm/V) :', G)
1 2 3 | |
Recherche des grandeurs caractéristiques pour un modèle du 1er ordre¶
On utilise les valeurs trouvées sur le premier dépassement pour déterminer les grandeurs caractéristiques du modèle de second ordre :
taula constante de temps du systèmetr5le temps de réponse à 5 %
Le modèle est de la forme :
# Recherche de la constante de temps
i_tau = np.where(mesure[debut:fin] >= Sinf*0.63)
tau = temps[i_tau[0][0]]
print('𝜏 (ms):', tau)
# Temps de réponse à 5%
i_tr5 = np.where(mesure[debut:fin] >= Sinf*0.95)
tr5 = temps[i_tr5[0][0]]
print('Tr5% (ms):', tr5)
tau_tr5 = tr5/3
print('𝜏 à partir du Tr5% (ms)', tau_tr5)
1 2 3 | |
Calcul de la réponse à un échelon du modèle¶
Utilisation du module signal pour calculer la réponse du modèle du premier ordre trouvé avec les deux \tau.
from scipy.signal import lti, step
# Déclaration de la fonction de transfert avec tau
ft1 = lti([G], [tau, 1])
# Déclaration de la fonction de transfert avec tau_tr5
ft2 = lti([G], [tau_tr5, 1])
# Calcul de la réponse
t1, y1 = step(ft1) # Réponse Indicielle modèle 1
y1 = y1 * E0
t2, y2 = step(ft2) # Réponse Indicielle modèle 2
y2 = y2 * E0
Affichage de la réponse du modèle¶
Affichage de la réponse du modèle superposé à la mesure.
# Affichage
plt.ylabel('Vitesse (rpm)') # Titre de l'axe y
plt.xlabel("Temps (ms)") # Titre de l'axe x
plt.title("Modèles et mesure") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.plot(temps[debut:fin]-temps[debut], mesure[debut:fin], label="Mesure")
plt.plot(t1, y1, label="Modèle 1")
plt.plot(t2, y2, label="Modèle 2 : tau basé sur Tr5% ")
plt.plot([0.0, tr5], [Sinf*0.95, Sinf*0.95],
'-r', label='95% de la valeur finale')
plt.plot([tr5, tr5], [0.0, Sinf*0.95], '-r')
plt.plot([0.0, tau_tr5], [Sinf*0.63, Sinf*0.63],
'--r', label='63% de la valeur finale')
plt.plot([tau_tr5, tau_tr5], [0.0, Sinf*0.63], '--r')
plt.legend()
plt.show()
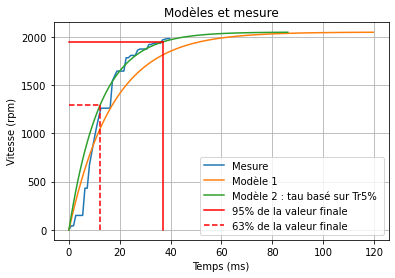
Au vu du tracé, le modèle 2 semble le plus proche de la mesure.
Système d'ordre 2¶
Les données mesurées sont stockées dans le fichier "Ordre2.csv".
Lecture des données¶
import numpy as np
# Lecture des en-têtes des données avec comme délimiteur le point-virgule
head = np.loadtxt('Ordre2.csv', delimiter=';', max_rows=1, dtype=np.str)
# Lecture des données au format str
data = np.loadtxt('Ordre2.csv', delimiter=';', skiprows=1, dtype=np.str)
# Affichage des en-têtes
print(head)
# Sélections des données en fonction de l'en-tête et conversion en flottant
# Le signe - adapte la donnée d'entrée pour quelle soit positive
temps = np.asarray(data[:, 0], dtype=np.float, order='C').flatten()
consigne = -np.asarray(data[:, 3], dtype=np.float, order='C').flatten()
mesure = -np.asarray(data[:, 1], dtype=np.float, order='C').flatten()
1 2 | |
import matplotlib.pyplot as plt # Module pour tracer les graphiques
plt.plot(temps, mesure, label="Position") # Ajout du d'une courbe avec label
plt.plot(temps, consigne, label="Consigne") # Ajout du d'une courbe avec label
plt.ylabel('Position (deg)') # Titre de l'axe y
plt.xlabel("Temps (ms)") # Titre de l'axe x
plt.title("Mesure brut") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.legend()
plt.show() # Affichage d'une courbe
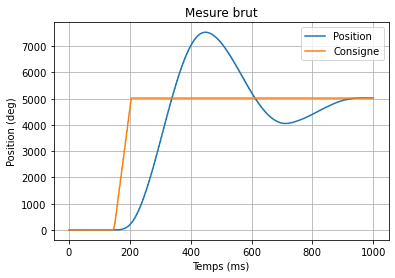
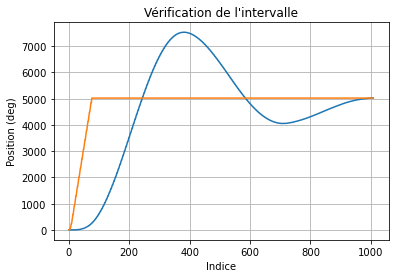
Identification début et fin de la réponse¶
Dans un premier temps on élimine les données inutiles (zone morte avant le début de l'action, temps d'acquisition trop long).
L'objectif est de trouver le début et la fin de la réponse du système.
# Recherche du début et de la fin en fonction de l'amplitude de la différence de la courbe
diff_mesure = np.diff(mesure)
diff_consigne = np.diff(consigne)
# La valeur de test est à adapter en fonction des cas
dt_mesure = np.where(diff_mesure > 1)
dt_consigne = np.where(diff_consigne > 1)
debut = dt_consigne[0][0] # Premier élement de l'intervalle
fin = dt_mesure[0][-1] # Dernier élément de l'intervalle
# Affichage
plt.ylabel('Position (deg)') # Titre de l'axe y
plt.xlabel("Indice") # Titre de l'axe x
plt.title("Vérification de l'intervalle") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.plot(mesure[debut:fin], label="Mesure")
plt.plot(consigne[debut:fin], label="Consigne")
plt.show()
Recherche des éléments caractéristiques de la réponse¶
On cherche les éléments caractéristiques des signaux :
E0consigne de l'échelonS_infvaleur finale de la mesureD1amplitude du premier dépassementT_D1temps au moment du premier dépassement
# Recherche de la consigne
E0 = consigne[-1]
print("Consigne (deg) :", E0)
# Calcul de la valeur final
S_inf = np.mean(mesure[fin:])
print("Valeur finale (deg) :", S_inf)
# Recherche du premier dépassement
D1 = np.max(mesure[debut:fin])
T_D1 = temps[np.argmax(mesure[debut:fin])]
print("Valeur premier dépassement (deg):", D1)
print("Instant du premier dépassement (ms) :", T_D1)
if T_D1 >= (temps[fin]-temps[debut])*0.95:
print("Régime critique ou apériodique")
modele = 3 # 0 = pseudo oscillatoire, 1 = critique, 2 = apériodique, 3 = critique ou apériodique
else:
print("Régime oscillatoire amorti")
modele = 0
1 2 3 4 5 | |
Recherche des grandeurs caractéristiques pour un modèle du second ordre¶
On utilise les valeurs trouvées sur le premier dépassement pour déterminer les grandeurs caractéristiques du modèle de second ordre :
mle coefficient d'amortissementomegala pulsation propreGgain statique de la réponse
Le modèle est de la forme :
Le temps au premier dépassement est :
Le premier dépassement (en %) est :
# Recherche du gain
G = S_inf/E0
print('Gain :', G)
# Cas du régime oscillatoire amorti
if modele == 0:
# Coefficient d'amortissement
D1_pourcent = abs((D1-S_inf)/(S_inf))
m = np.sqrt((np.log(D1_pourcent)**2)/(np.pi**2+np.log(D1_pourcent)**2))
print("Coefficient d'amortissement :", m)
# Recherche de la pulsation propre
if m > 1:
print("Régime apériodique")
modele = 2
elif m == 1:
print("Régime critique")
modele = 1
else:
print("Régime oscillatoire amorti")
omega = np.pi/(T_D1*np.sqrt(1-m**2))
print("Pulsation (rad/s) :", omega)
# Autres modèles
if modele == 3 or modele == 2 or modele == 1:
# Recherche de la constante de temps
i_tau = np.where(mesure[debut:fin] >= Sinf*0.63)
tau = temps[i_tau[0][0]]
print('𝜏 (ms):', tau)
# Temps de réponse à 5%
i_tr5 = np.where(mesure[debut:fin] >= Sinf*0.95)
tr5 = temps[i_tr5[0][0]]
print('Tr5% (ms):', tr5)
if tr5/3 <= tau*1.05 and tr5/3 >= tau*0.95:
modele = 1
else:
modele = 2
1 2 3 4 | |
Calcul de la réponse à un échelon du modèle¶
Utilisation du module signal pour calculer la réponse du modèle du second ordre trouvé
from scipy.signal import lti, lsim, step
if modele == 0:
# Déclaration de la fonction de transfert
ft = lti([G], [1/omega**2, 2*m/omega, 1])
elif modele == 1:
ft = lti([G], [(tr5/3)**2, 2*tr5/3, 1])
elif modele == 2:
print("Valeurs de tau1 et tau2 à redéfinri à la main")
tau1 = tau/10 # A définir
tau2 = tr5/3 # A définir
ft = lti([G], [tau1*tau2, tau1+tau2, 1])
# Calcul de la réponse
t = temps[debut:fin]-temps[debut]
u = consigne[debut:fin]
if modele < 3:
t1_ft, y1, _ = lsim(ft, U=u, T=t) # Réponse à la consigne
t2_ft, y2 = step(ft) # Réponse indicielle
y2 = y2 * E0
else:
print("Aucun modèle valide")
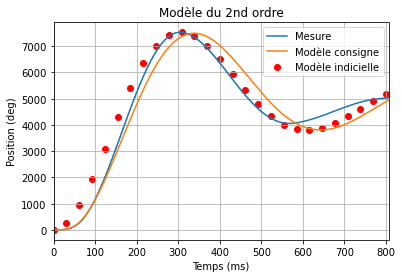
Affichage de la réponse du modèle¶
Affichage de la réponse du modèle superposé à la mesure.
# Affichage
plt.ylabel('Position (deg)') # Titre de l'axe y
plt.xlabel("Temps (ms)") # Titre de l'axe x
plt.title("Modèle du 2nd ordre") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.plot(temps[debut:fin]-temps[debut], mesure[debut:fin], label="Mesure")
plt.plot(t1_ft, y1, label="Modèle consigne")
plt.scatter(t2_ft, y2, label="Modèle indicielle", color='red')
plt.xlim(t[0], t[-1])
plt.legend()
plt.show()
Ajustement de la pulsation propre¶
from scipy.signal import lti, lsim, step
# Modification de la pulsation
omega2 = omega+0.0012
# Déclaration de la fonction de transfert
ft = lti([G], [1/omega2**2, 2*m/omega2, 1])
t_ft, y, _ = lsim(ft, U=u, T=t) # Réponse à la consigne
# Affichage
plt.ylabel('Position (deg)') # Titre de l'axe y
plt.xlabel("Temps (ms)") # Titre de l'axe x
plt.title("Modèle du 2nd ordre") # Titre du graphique
plt.grid(True) # Affichage de la grille
plt.plot(temps[debut:fin]-temps[debut], mesure[debut:fin], label="Mesure")
plt.plot(t_ft, y, label="Modèle ajusté")
plt.legend()
plt.show()
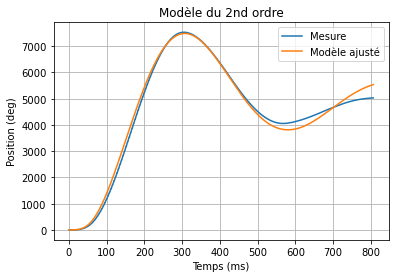
Après ajustement, on est bien plus proche de la mesure.